Il fenomeno è certo importante ma ingiustamente sottovalutato. Nel contesto della logica digitale con il termine metastabilità ci si riferisce alla capacità dei sistemi di risolvere da stati poco stabili a stati più stabili. Sebbene la definizione sia univoca non risulta molto chiara. Infatti molti progettisti considerano i sistemi digitali come soggetti a solo due stati, il classico valore "0" ed "1", ma in realtà i circuiti che operano memorizzando un dato elementare esibiscono tre stati. Si consideri un semplice circuito con flip-flop di tipo D come in figura:

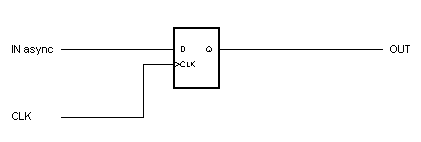
Un circuito che evidenzia un comportamento metastabile

Vi sono due linee di ingresso, una dedicata a dati asincroni (D) ed una per il segnale di clock (CLK) che controlla il circuito. La linea di uscita (Q) si porta al valore dell'ingresso dati quando il segnale di clock ha una transizione verso l'alto e mantiene questo valore fino al successivo fronte di salita di clock. L'informazione è quindi memorizzata tra questi due eventi. Il comportamento descritto è tipico di questa classe di circuiti e particolarmente del dispositivo standard 7474 nelle sue molte varianti.

Il flip-flop di tipo D è un tipico esempio di sistema con retroazione nel quale uno o più dei segnali di uscita è riportato in uno o più ingressi. La figura mostra il diagramma interno del 7474 dal quale risulta chiaro questa interazione tra linee di segnale:

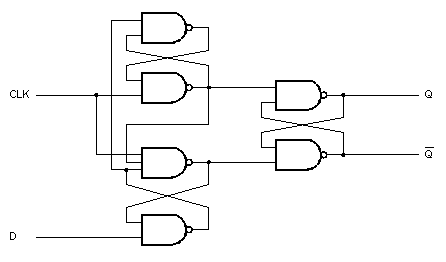
Schema interno di un flip-flop tipo D

Rappresentiamo quindi i diversi segnali ponendo che l'ingresso asincrono D sia ad "1" nell'instante in cui il clock ha una transizione verso l'alto, l'uscita in questo caso si porterà ad "1" ed in tale stato rimarrà indipendentemente dalla condizione di ingresso.

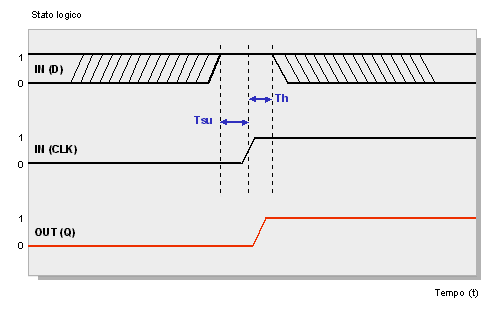
Segnali in un flip-flop tipo D

Osserviamo che in riferimento alla transizione di clock il setup time (Tsu) ed il hold time (Th) definiscono assieme il periodo nel quale l'ingresso D deve aver già raggiunto e mantenuto la condizione definitiva. Qualora vi sia una violazione di questa tempistica in un flip-flop l'uscita non è predicibile, questo stato è conosciuto come metastabile. Al termine della fase metastabile l'uscita del flip-flop si porta ad uno dei due valori stabili "0" oppure "1". Il processo nel suo insieme prende il nome di metastabilità. Il periodo nel quale permane il fenomeno dipende dalla tecnologia della famiglia di dispositivi usati.

Se osserviamo le dinamiche interne al dispositivo vediamo che lo stato metastabile si presenta quando vi è una violazione del setup time oppure del hold time. In tali circostanze il fronte di salita del clock avviene in concomitanza, anche parziale, con la transizione sull'ingresso D. I percorsi dei segnali interessano coppie di NAND connessi come latch principali (master) e secondari (slave), accade cosi nella peggiore ipotesi che l'elemento master cerca nella transizione di CLK di catturare lo stato attivo in quell'istante mentre all'elemento slave è consentito sulla uscita Q di seguire il valore del latch principale. Idealmente vi sono le condizioni per un equilibrio che richiede al flip-flop un certo tempo per raggiungere uno degli stati stabili.

Possiamo immaginare questa condizione come un sistema che cerca di portarsi al suo minimo livello di energia, stato "0" oppure "1", ma che presenta una zona intermedia a livello maggiore. Il sistema cerca di fare cadere la condizione in uno dei due stati minimi ma se il punto di partenza è spostato rispetto il punto finale ci vorrà del tempo affinché questo venga raggiunto, se poi il punto di partenza è grossomodo in equilibrio (metastabile) il tempo richiesto sarà molto maggiore. Questo scenario diviene intuibile guardando la figura seguente con la condizione logica rappresentata da una pallina che può trovarsi ai piedi di un rilievo, ed essere pertanto stabile, oppure prossima al vertice nel qual caso dovrà ricadere su uno dei lati.

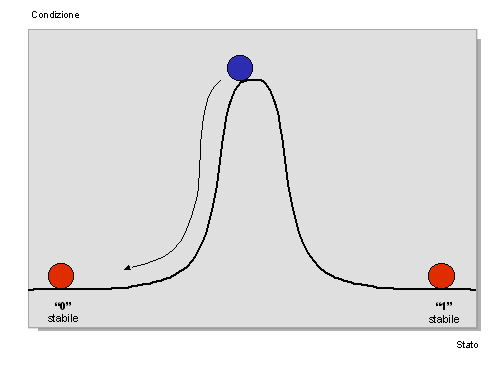
Rappresentazione del fenomeno metastabile

E' opportuno evidenziare che il tempo impiegato dal sistema per raggiungere una condizione stabile dipende dal punto iniziale nel quale viene a trovarsi. Rimanendo alla rappresentazione portata ad esempio qualora la pallina venga posta in prossimità della base del rilievo impiegherà poco tempo per fermarsi al suo estremo, al contrario se venisse posta esattamente al vertice si troverebbe in uno stato di equilibrio precario ma di durata anche infinita in linea di principio. Nella realtà questo non può accadere in quanto il rumore termico all'interno del dispositivo sposta la condizione di poco ma abbastanza per fare cadere la pallina (tensione) su uno dei lati (soglie logiche), in quale non siamo in grado di predirlo.

E' interessante notare che spostando l'attenzione da questo esempio alla realtà fisica intrinseca ai dispositivi digitali lo stato metastabile corrisponde ad un punto intermedio di tensione tra i livelli alto e basso. Per una struttura CMOS bilanciata, con transistor a canale N e P di uguali caratteristiche, porta ad identificare il vertice del rilievo con una tensione di 1/2 VCC ovvero al punto di incrocio delle forme d'onda durante la transizione tra condizioni logiche diverse. In questa zona i dispositivi digitali possono essere considerati dei sistemi lineari per piccoli segnali, dei circuiti analogici a tutti gli effetti dunque, descritti con equazioni di correnti, tensioni, resistenze e reattanze. Adottando alcune semplificazioni il latch di cui è costituito il flip-flop può essere visto nel suo modello equivalente composto da due amplificatori invertenti, ognuno associato ad una definita costante di tempo, posti in cascata e connessi così che venga a crearsi una retroazione positiva.

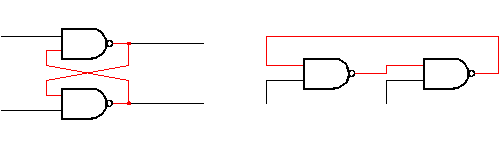
Un latch e sua ridisposizione per evidenziare la retroazione tra NAND in serie

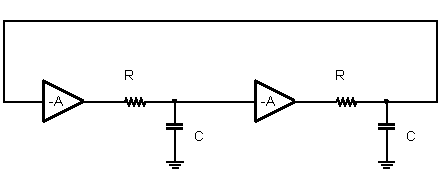
Modello per piccoli segnali di un latch nella regione di incrocio delle forme d'onda

Gli amplificatori sono contraddistinti da un fattore di amplificazione in tensione A con R che ne rappresenta la resistenza di uscita e C la somma delle capacità sul nodo verso massa. Sostanzialmente sono i parametri della rete interna del circuito integrato. Scrivendo le equazioni che descrivono l'andamento della tensione sui nodi in funzione del tempo si ha modo di constatare che è presente un termine esponenziale. Questo termine ci dice quanto veloce sarà il circuito a portarsi fuori dalla regione metastabile. Quanti progettano circuiti digitali in ambito professionale devono rammentare tale dettaglio, l'analisi / simulazione che ne segue integra infatti il termine che trae origine e giustificazione dal modello analogico del componente digitale.

Tutte le novità, promozioni, sconti del periodo