
Parametri caratteristici dei filtri
| « Pagina precedente | Indice FILTRI ATTIVI | Pagina seguente » |
Prima di sviluppare il progetto di un filtro è di primaria importanza definirne i parametri caratteristici di funzionamento, questo significa impostare quale risposta deve presentare nel dominio della frequenza e del tempo. Va sottolineato che i filtri, come tipologia di circuiti, richiederebbero complesse nozioni matematiche per una analisi dettagliata del loro comportamento. Non solo, a seconda dell'ambito di applicazione talune nozioni assumono più o meno rilievo richiedendo pertanto un approfondimento specifico. Fortunatamente accettando alcune semplificazioni risulta possibile adottare un approccio che si basa su definizioni standard, valide nella pratica per buona parte delle situazioni reali. A seguire tra le diverse tipologie di filtro privilegeremo nella trattazione il tipo passa-basso, sen'altro la forma più diffusa. Quanto illustreremo con pochi adattamenti avrà poi validità generale indipendentemente dalla struttura del filtro. Una rete passa-basso può essere specificato in termini di quattro parametri, la figura gli mostra graficamente evidenziando le diverse aree che socchiudono:
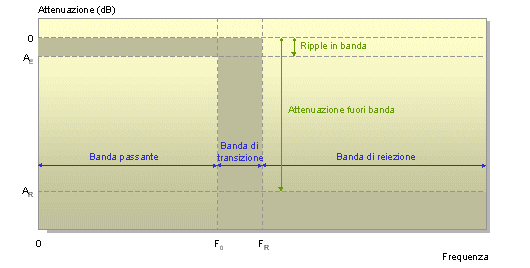
Termini limite di un filtro passa-basso
Il significato dei termini è come segue. Frequenza di taglio (Fo), la frequenza alla quale la risposta del filtro supera il segmento in banda passante che tipicamente corrisponde a -3 dB per i filtri Butterworth. Frequenza di reiezione (Fr), la frequenza alla quale la risposta del filtro raggiunge la minima attenuazione richiesta nella banda di reiezione. Ripple in banda (Ae), la massima attenuazione ammessa nel segmento in banda passante corrispondende a -3 dB per i filtri Butterworth. Attenuazione fuori banda (Ar), la minima attenuazione richiesta nella banda di reiezione. Da notare che abbiamo volutamente citato i filtri Butterworth in quanto una tipologia molto diffusa.
In un progetto concreto non tutti questi parametri hanno uguale importanza. Ad esempio il ripple in banda potrebbe essere un fattore primario nelle applicazioni audio di alta qualità dove si vuole alterare il meno possibile la risposta inferiore ai canonici 20kHz. Nei filtri a banda medio/stretta invece è la riduzione della banda di transizione spesso il fattore chiave. Il grafico poco sopra proposto ci offre i limiti entro cui la risposta in frequenza deve ricadere, un ipotetico filtro passa-basso che risponde ai requisiti che abbiamo imposto è visibile nella figura seguente:
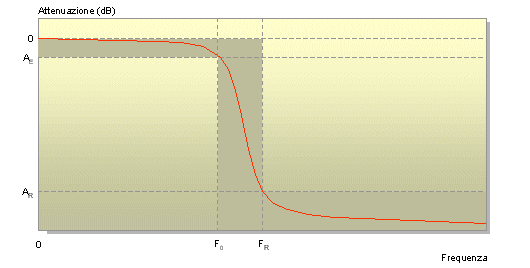
Termini operativi di un filtro reale passa-basso
La linea di colore rosso disegna la curva di risposta della rete, dato che si trova entro i limiti di progetto si dimostra adatta alle nostre esigenze. Ma attenzione, come è intuibile vi sono diversi tipi di risposta in frequenza che possono soddisfare i requisiti per ogni particolare filtro. Quattro famiglie principali si distinguono per caratteristiche proprie:
| Tipo di Risposta | Ripple in banda | Pendenza (*) |
|
Bessel
Presenta la più lineare risposta in fase in banda passante, a scapito di una bassa pendenza di attenuazione oltre la frequenza di taglio |
3 dB | <6 dB/ottava |
|
Butterworth
Presenta il miglior compromesso tra attenuazione e risposta in fase. Non ha ondulazioni in banda passante a spese di una relativamente ampia banda di transizione. E' il tipo di risposta più usato |
3 dB | 6 dB/ottava |
|
Chebyshev
Presenta una elevata selettività, ovvero una maggiore pendenza di attenuazione oltre la frequenza di taglio. Ha ondulazioni in banda passante |
>0 dB | >6 dB/ottava |
|
Ellittica
Presenta la più elevata selettività, ovvero la maggiore pendenza di attenuazione oltre la frequenza di taglio, a scapito di una degradata risposta in fase. Ha ondulazioni sia nella banda passante che nella banda di transizione |
>0 dB | >6 dB/ottava |
L'asterisco indica che la pendenza nella banda di transizione, qui presa a riferimento, concerne le reti di 1° ordine. Da notare che nei filtri Bessel e Butterworth la frequenza di taglio Fo è per definizione coincidente con il punto ove l'attenuazione assume il valore di 3 dB. Per i filtri Chebyshev ed Ellittici invece si considera il punto ove si supera il valore di ripple, questo è imposto dal progetto essendo una variabile e non una caratteristica intrinseca al tipo di risposta. La pendenza di attenuazione lontano dalla frequenza di taglio per tutti i filtri, ad esclusione degli Ellittici, è sempre data dalle seguenti relazioni:

Dove AL è la pendenza di attenuazione in dB, N è l'ordine del filtro, Ottava indica un intervallo di frequenze con rapporto max/min pari a 2, Decade indica un intervallo di frequenze con rapporto max/min pari a 10. Osservate che nella banda di transizione, cioè subito dopo la frequenza di taglio, ogni filtro ha un comportamento diverso come indicato nell'ultima voce della tabella riassuntiva proposta poco sopra. Per meglio quantificare la differenza tra le diverse risposte il grafico che segue mostra l'andamento della curva di attenuazione per filtri di 5° ordine con frequenza di taglio di 50 KHz rispettivamente per il tipo Butterworth, Chebyshev con ripple di 3 dB, Bessel:

Filtri con diversa risposta
L'ordine del filtro, in altri termini il fattore che determina l'ammontare della pendenza di attenuazione, dipende dal numero di componenti utilizzati. Con un solo amplificatore operazionale è possibile realizzare filtri di 1° e di 2° ordine, non oltre. Il filtro di 5° ordine cui si riferiscono le risposte in frequenza del grafico precedente è quindi realizzato con un minimo di tre amplificatori operazionali ognuno adeguatamente supportato da reti composte da resistenze e condensatori. Nella sostanza tre sezioni poste in serie.
La differenza tra le risposte viene ottenuta scegliendo opportunamente il fattore di smorzamento di ogni sezione, questo parametro (indicato con a) esprime la tendenza del circuito a creare oscillazioni in risposta a segnali impulsivi. Con diversa interpretazione matematica in molti casi invece del fattore a viene usato il fattore di qualità del filtro (indicato con Q) che esprime il medesimo concetto ma con scale opposte: si ottiene una elevata tendenza alle oscillazioni quando a è minore di 1, od in maniera equivalente, quando Q è maggiore di 1. Per simmetria vediamo ora il filtro passa-alto, anch'esso può essere specificato in termini di quattro parametri, la figura gli mostra graficamente evidenziando le diverse aree che socchiudono:
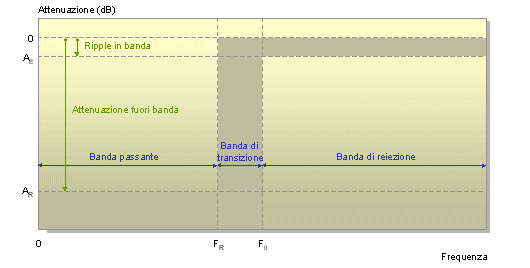
Termini limite di un filtro passa-alto
Il significato dei termini è come segue. Frequenza di taglio (Fo), la frequenza alla quale la risposta del filtro raggiunge il segmento in banda passante, tipicamente corrisponde a -3 dB per i filtri Butterworth. Frequenza di reiezione (Fr), la frequenza alla quale la risposta del filtro supera la minima attenuazione richiesta nella banda di reiezione. Ripple in banda (Ae), la massima attenuazione ammessa nel segmento in banda passante, corrisponde a -3 dB per i filtri Butterworth. Attenuazione fuori banda (Ar), la minima attenuazione richiesta nella banda di reiezione. Se questo è per il passa-alto molto cambia per il filtro passa-banda, per essere specificato occorrono ora più parametri in parte interdipendenti. La figura gli mostra graficamente evidenziando le diverse aree che socchiudono:
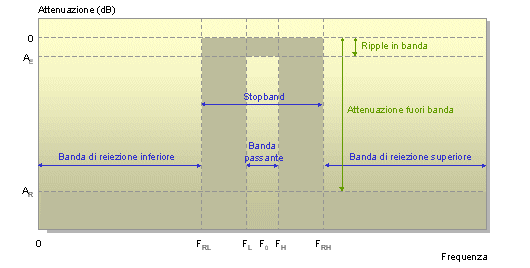
Termini limite di un filtro passa-banda
Il significato dei termini è come segue. Frequenza centrale (Fo), frequenza al centro della banda passante, è uguale alla media geometrica delle frequenze di taglio inferiore e superiore. Frequenza di taglio inferiore (FL), la frequenza alla quale la risposta del filtro raggiunge il segmento in banda passante, tipicamente corrisponde a -3 dB per i filtri Butterworth. Frequenza di taglio superiore (FH), la frequenza alla quale la risposta del filtro supera il segmento in banda passante, tipicamente corrisponde a -3 dB per i filtri Butterworth. Frequenza di reiezione inferiore (FRL), la frequenza alla quale la risposta del filtro supera la minima attenuazione richiesta nella banda di reiezione. Frequenza di reiezione superiore (FRH), la frequenza alla quale la risposta del filtro raggiunge la minima attenuazione richiesta nella banda di reiezione. Ripple in banda (Ae), la massima attenuazione ammessa nel segmento in banda passante, corrisponde a -3 dB per i filtri Butterworth. Attenuazione fuori banda (Ar), la minima attenuazione richiesta nella banda di reiezione. Va precisato che nella sua forma più semplice il filtro passa-banda richiede una caratterizzazione con meno parametri e di interpretazione più immediata. La figura seguente gli mostra nel caso di una curva di risposta derivante da un circuito a singola cella, la struttura meno complessa in assoluto:
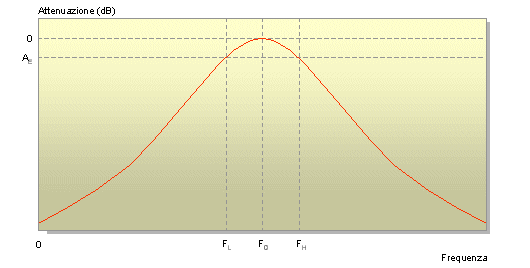
Termini base di un filtro passa-banda
Il valore di Ae è per definizione in questo caso sempre di -3 dB, il segmento della curva entro la banda passante è in relazione alla frequenza centrale (Fo) tramite il fattore di qualità Q che caratterizza il filtro, più il Q è elevato e maggiormente il filtro è selettivo. Di seguito alcune formule di uso universale per questo tipo circuiti:
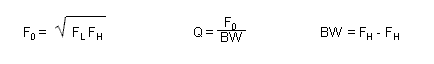
Dove Fo è la frequenza centrale in Hz, FL la frequenza di taglio inferiore in Hz, FH la frequenza di taglio superiore in Hz, Q è il fattore di qualità, BW infine è la larghezza della banda passante sempre in Hz. Per simmetria vediamo ora il filtro elimina-banda, per essere specificato occorrono più parametri in parte interdipendenti, la figura gli mostra graficamente:
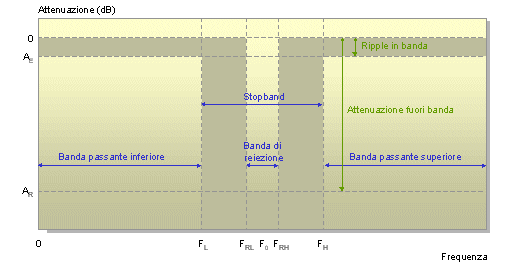
Termini limite di un filtro elimina-banda
Il significato dei termini è come segue. Frequenza centrale (Fo), frequenza al centro della banda passante, è uguale alla media geometrica delle frequenze di taglio inferiore e superiore. Frequenza di taglio inferiore (FL), la frequenza alla quale la risposta del filtro supera il segmento in banda passante, tipicamente corrisponde a -3 dB per i filtri Butterworth. Frequenza di taglio superiore (FH), la frequenza alla quale la risposta del filtro raggiunge il segmento in banda passante, tipicamente corrisponde a -3 dB per i filtri Butterworth. Frequenza di reiezione inferiore (FRL), la frequenza alla quale la risposta del filtro raggiunge la minima attenuazione richiesta nella banda di reiezione. Frequenza di reiezione superiore (FRH), la frequenza alla quale la risposta del filtro supera la minima attenuazione richiesta nella banda di reiezione. Ripple in banda (Ae), a massima attenuazione ammessa nel segmento in banda passante, corrisponde a -3 dB per i filtri Butterworth. Attenuazione fuori banda (Ar), la minima attenuazione richiesta nella banda di reiezione. Come per il caso precedente nella sua forma più semplice il filtro elimina-banda richiede una caratterizzazione con meno parametri e di interpretazione più immediata. La figura gli mostra nel caso di una curva di risposta derivante da un circuito a singola cella filtrante:
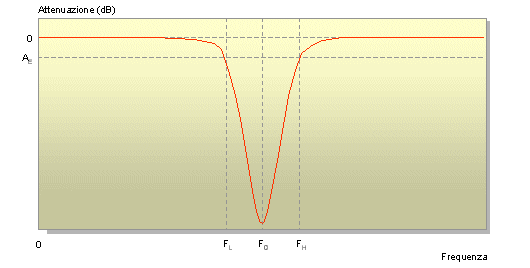
Termini base di un filtro elimina-banda
Il valore di Ae risulta per definizione in questo caso sempre di -3 dB, il segmento della curva entro la banda di reiezione è in relazione alla frequenza centrale (Fo) tramite il fattore di qualità (Q) che caratterizza il filtro, di nuovo più il Q è elevato e maggiormente il filtro si definisce selettivo. Di seguito alcune formule di uso universale per questo tipo circuiti:
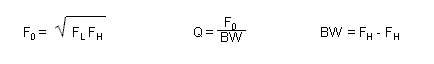
Dove Fo è la frequenza centrale, FL la frequenza di taglio inferiore, FH la frequenza di taglio superiore, Q il fattore di qualità, BW la larghezza della banda passante. Tutte le frequenze in Hz naturalmente. Con questo concludiamo il post, per approfondire i singoli circuiti che realizzano filtri con amplificatori operazionali vi invitiamo a consultare le altre pagine del sito.
| « Pagina precedente | Indice FILTRI ATTIVI | Pagina seguente » |
Info Zone
Tutte le novità, promozioni, sconti del periodo