Nel descrivere i principi su cui operano i filtri a capacità commutate (SC), switched capacitor nella terminologia inglese, seguiamo il percorso evolutivo che porta dai filtri attivi realizzati con amplificatori operazionali e reti RC già analizzati in altre parti di questo sito alle equivalenti reti a commutazione. Quale riferimento circuitale prendiamo il più comune dei filtri attivi RC, il tipo passa-basso con risposta di 2° ordine, che riportiamo in figura.

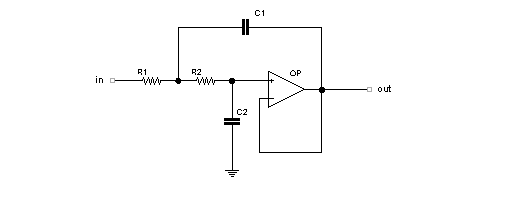
Cella passa-basso con operazionale

Questo circuito presenta una pendenza di attenuazione di 12 dB/ottava nel tratto della curva di risposta oltre la frequenza di taglio, in questa regione ad ogni raddoppio della frequenza il segnale diminuisce quindi di ampiezza per un valore di 12 dB. La frequenza di taglio F0 viene data dalla seguente relazione.

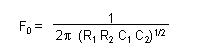
Dove Fo è la frequenza di taglio (in Hz), le resistenze sono in ohm mentre i condensatori in Farad.

L'implementazione di questo semplice circuito non presenta difficoltà nel caso si mantenga F0 fisso ad una determinata frequenza, desiderando però variare questo parametro entro un specifico intervallo di valori si deve modificare simultaneamente il valore delle resistenze R1 ed R2 tramite l'impiego di un trimmer oppure un potenziometro doppio. E' possibile ottenere il medesimo risultato variando simultaneamente il valore dei condensatori C1 ed C2 anzichè delle resistenze ma questa eventualità non trova pratica realizzazione. Constatiamo che avendo come unica possibilità l'uso di un potenziometro doppio per regolare F0 per il filtro indicato tale soluzione non presenta significativi problemi, questi invece si presentano quasi insormontabili nel caso di filtri di ordine maggiore caratterizzati da una più elevata pendenza di attenuazione.

Per questi circuiti infatti sarebbe necessario disporre di un potenziometro con un numero di sezioni pari all'ordine del filtro così da poterne variare la frequenza agendo contemporaneamente in tutte le celle elementari che lo costituiscono. La difficoltà meccanica intrinseca a questa soluzione e le differenze, inevitabili, nel valore di resistenza tra le diverse sezioni rende questa modalità di regolazione non proponibile. Si deve pertanto trovare una soluzione alternativa per ottenere i medesimi risultati senza che insorgano i citati inconvenienti.

Tale alternativa è stata identificata nella tecnica delle resistenze commutate (SR) che consente di variare il valore di una resistenza agendo tramite un controllo remoto su uno, o più, deviatori collegati in diversa forma al componente in questione. Nella figura seguente si osserva la più semplice di queste configurazioni SR con la resistenza ed il deviatore posti in parallelo:

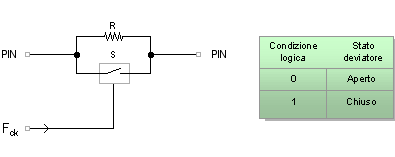
Agendo sul segnale di clock Fck che controlla lo stato del commutatore è intuibile che quando questo è aperto, per una condizione logica 0, tra i terminali si riscontra esclusivamente il valore della resistenza R. Quando invece agendo sul segnale di clock il commutatore è chiuso, per una condizione logica 1, la resistenza viene cortocircuitata così che tra i terminali riscontriamo un valore zero. Questo naturalmente supponendo il deviatore come un componente ideale, ipotesi adeguata all'attuale livello di descrizione.

Introduciamo ora il concetto di duty-cycle di Fck, parametro che definisce il rapporto tra il tempo nel quale il segnale è in condizione logica 1 (t1) ed il periodo completo di un ciclo del segnale di clock (T), nella forma analitica abbiamo quindi:

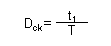
Dove Dck è il duty-cycle del segnale di clock, t1 il periodo in condizione logica alta e T il periodo di un intero ciclo del segnale.

La stessa relazione si può esprimere con una percentuale:

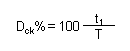
Dove Dck% è il duty-cycle in percentuale del segnale di clock, t1 il periodo in condizione logica alta e T il periodo di un intero ciclo del segnale.

Se manteniamo costante Fck e variamo il duty-cycle tra gli estremi zero e 100% otteniamo una corrispondente modifica nel rapporto dei tempi che vede connessa tra i terminali del nostro circuito una resistenza di valore R e zero. Se consideriamo l'andamento del valore della resistenza equivalente Req su una base temporale maggiore di T, in altri termini eseguendo una media che tenga conto sia di quando il commutatore è aperto sia di quando è chiuso, la possiamo ritenere intermedia tra R e zero in relazione diretta al duty-cycle del segnale di controllo. Numericamente otteniamo:

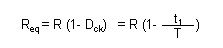
Dove Req è la resistenza equivalente, R la resistenza inserita nel circuito, Dck è il duty-cycle del segnale di clock, t1 il periodo in condizione logica alta e T il periodo di un intero ciclo del segnale.

E' interessante mostrare l'andamento di Req in funzione di Dck come si ricava dalla relazione ora presentata, il grafico che segue ne presenta le caratteristiche dal quale si evince come variando il duty-cycle possiamo ottenere qualsiasi valore della resistenza equivalente a partire da R a scendere:

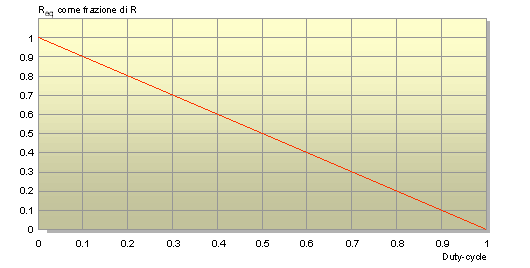
Valore della resistenza commutata in funzione del duty-cycle

Quale esempio con R di 4700 ohm variando Dck otteniamo la scala di valori della resistenza equivalente qui raffigurata:

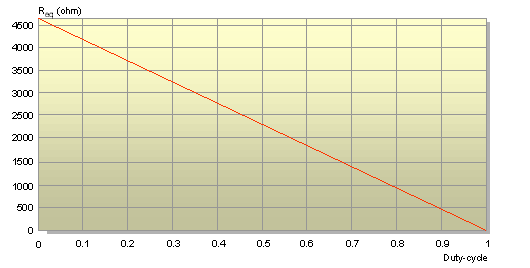
Valore della resistenza da 4700 ohm in funzione del duty-cycle

Importante, il termine media cui ci riferiamo considerando l'andamento del valore della resistenza in un periodo maggiore di T ha primaria importanza in questo ed in tutti i circuiti sottoposti a campionamento o commutazione periodica. In altra pagina del sito viene analizzato nel dettaglio tale aspetto, per la descrizione base che stiamo ora portando avanti si consideri semplicemente valida la definizione di Req senza soffermarci sulle sue altre implicazioni.

Una variante al circuito proposto consiste nel collegare la resistenza ed il deviatore in serie anzichè in parallelo:

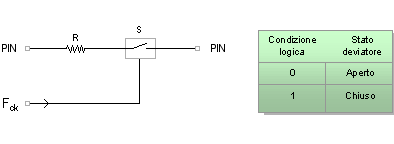
Agendo sul segnale di clock Fck che controlla lo stato del commutatore è intuibile che quando questo è aperto, per una condizione logica 0, tra i terminali si riscontra un valore di resistenza infinito. Quando invece agendo sul segnale di clock il commutatore è chiuso, per una condizione logica 1, la sola resistenza R appare tra i terminali. Questo naturalmente supponendo il deviatore come un componente ideale. Analogamente a quanto già visto in precedenza variando il duty-cycle tra gli estremi zero e 100% otteniamo una corrispondente modifica nel rapporto dei tempi che vede connessa tra i terminali del nostro circuito una resistenza di valore infinito ed R. Numericamente il valore di Req in funzione di Dck è dato dalla relazione:

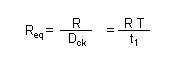
Dove Req è la resistenza equivalente, R la resistenza inserita nel circuito, Dck è il duty-cycle del segnale di clock, t1 il periodo in condizione logica alta e T il periodo di un intero ciclo del segnale.

Il grafico che segue ne presenta le caratteristiche dal quale si evince come variando il duty-cycle possiamo ottenere qualsiasi valore della resistenza equivalente a partire da R a salire.

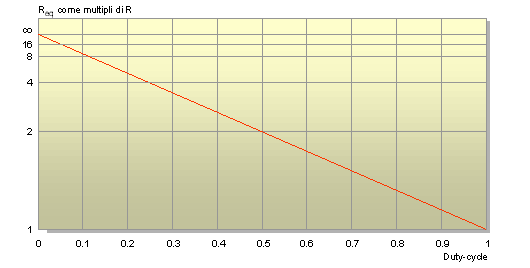
Valore della resistenza commutata in serie in funzione del duty-cycle

Quale esempio con R di 4.7 Kohm ohm variando Dck otteniamo la scala di valori della resistenza equivalente qui raffigurata:

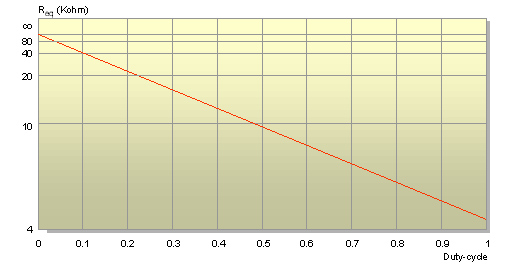
Valore della resistenza da 4.7 kohm in funzione del duty-cycle

I circuiti a SR presentati impiegano un solo deviatore e sono la più semplice forma di realizzazione per questa tecnologia. Sono possibili naturalmente schemi di maggiore complessità che consentono di superare i limiti associati all'intervallo di variazione della Req che come abbiamo osservato per le versioni proposte non può essere contemporaneamente inferiore e superiore al valore di R.

Compresi i principi su cui poggiano il funzionamento tali circuiti il passo immediatamente seguente è di integrarli nelle tipologie tradizionali, quale riferimento circuitale prendiamo nuovamente il passa-basso con risposta di 2° ordine citato ad inizio pagina, eccolo in figura:

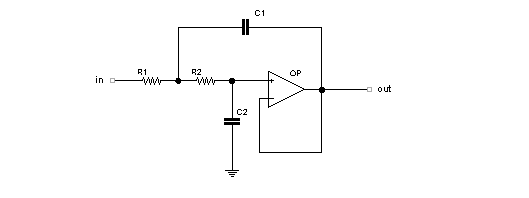
La cella passa-basso con amplificatore operazionale

Ricordiamo che questo circuito definito per una risposta di tipo Butterworth presenta una pendenza di attenuazione di 12 dB/ottava. Tale filtro può essere riproposto sostituendo le resistenze fisse R1 e R2 con due reti SR ottenendo il controllo di Req in maniera similare alla variazione che si avrebbe agendo tramite un doppio potenziometro meccanico. Con questa sostituzione operando simultaneamente su entrambi i deviatori si sposta a piacimento la frequenza di taglio F0 del filtro, il duty-cycle del segnale di clock Fck in altri termini controlla il comportamento in frequenza del circuito. In figura il filtro SR passa-basso con risposta di 2° ordine:

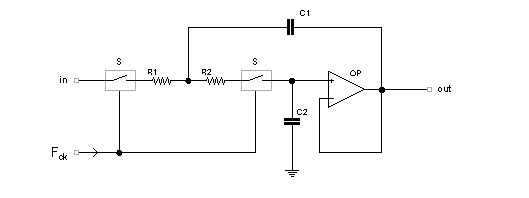
Cella passa-basso in tecnologia a resistenze commutate

Il vantaggio principale intrinseco in questa configurazione circuitale risiede nella facilità, e comodità, di regolazione del parametro F0 del filtro anche nel caso di più celle in cascata per ottenere una pendenza di attenuazione maggiore di 12 dB/ottava oltre la frequenza di taglio. Viene meno pertanto la gravosa necessità di utilizzare un potenziometro con sezioni multiple semplificando la realizzazione del circuito da una parte e offrendo dall'altra una minore differenza di prestazioni tra le diverse Req così da creare le condizioni per un miglioramento della precisione del filtro nel suo complesso.

La tecnologia attuale ad alta integrazione sostituisce i deviatori con dei dispositivi MOSFET presenti nello stesso chip monolitico che include l'amplificatore o gli amplificatori operazionali delegando all'esterno la sola regolazione della frequenza di taglio. Si può pertanto realizzare filtri con risposte di ordine elevato utilizzando un singolo circuito integrato complesso nel quale fornire quali input i parametri che ne determinano le caratteristiche, quindi la F0 ma anche il fattore di merito ed il guadagno.

Oltre il filtro passa-basso proposto sin qui quale ulteriore esempio la tecnica SR può andare a sostituire i componenti tradizionali per realizzare altri circuiti filtranti controllati dalla Fck. In figura il tipo passa-alto con risposta di 2° ordine nella variante SR:

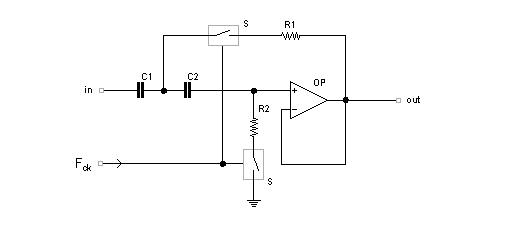
Cella passa-alto in tecnologia a resistenze commutate

Analogamente a quanto visto sin d'ora l'uso della tecnologia a resistenze commutate può essere integrata nei filtri passa-banda e notch, in questi casi non solo per controllare la frequenza centrale ma pure la larghezza di banda dei circuiti.

Tutte le novità, promozioni, sconti del periodo